Sides & Angles: The Thrilling world of Triangles in geometry
Triangles! The building blocks or architects of the geometric world. The three corners or sides and three angles of the triangle combined in different forms to create new shapes. From the manly created pyramids to nature’s created stars. Mathematicians and artists are kept under the cage of triangles. Let’s dive into the thrilling world of triangles in geometry.
In this article we will discuss about the Sides & Angles: The Thrilling world of Triangles in geometry.
Basic Introduction Of Triangles
The simple definition of triangle is: “a polygon or a geometric shape that has three sides, three angles or three vertices. The angle when measured is equivalent to 180°. In other words, the sum of interior angles or addition of interior angles is equivalent to 180°. It’s a 2D structure.
Classification of Triangles by Sides And Angles
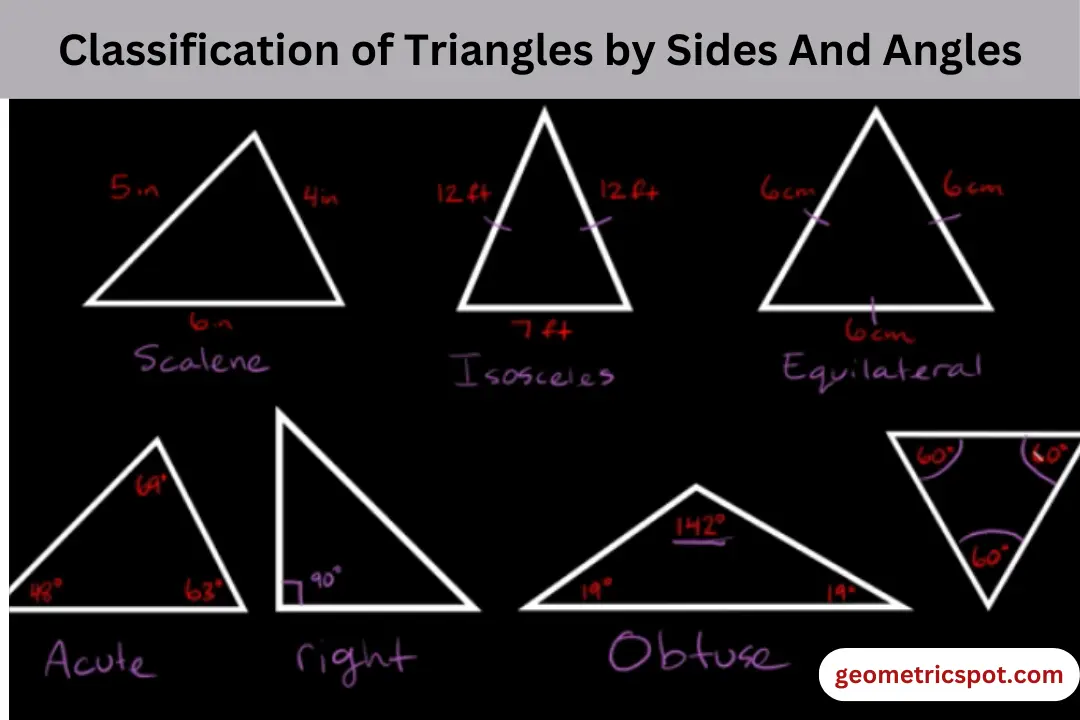
Triangles are majorly classified into 6 different types based on the sides and angles. Just imagine a three legged-stool, that’s the beauty of a triangle. It is made by three lines connecting three vertices. They are the simplest shapes in the world of geometry. Let’s read the further classification of the thrilling world of triangles.
The ABCs of triangles based on the length of the sides:
Side
We can simply say that sides of the triangle are straight lines that meet each other at the vertices.
- Equilateral Triangle – All the sides of the triangle are equal in length in measurement. For example; Imagine about a pyramid. It’s the perfect example of an equilateral triangle.
- Isosceles Triangle – Any two sides of a triangle are equal in length. For example; Imagine a slice of pizza. 2 sides are equal in length while one is different in size.
- Scalene Triangle – Any two sides are unequal in length. In other words, all three sides have different sizes of length when measuring. For example; imagine a triangle we usually draw without scale. It’s almost a scalene triangle.
The ABCs of triangles based on the angles:
Angle
The measurement of interior angles of the triangle should be 180°. We can also classify triangles based on angles just like angles themselves.
- Acute Triangle – All the three sides or angles should be less than 90°. For example; 80°, 20°, or 30°. Imagine a mountain with a pointy peak. That’s exactly an acute triangle.
- Right Triangle – Right angle triangle means one side should be equal to exactly 90°. For example; imagine a square shaped bread cut into a triangle, one side is straight and exactly 90°.
- Obtuse Angle – Angle that lies between 90° and 180° is known as the obtuse angle triangle. In other words, one side of the triangle or angle should be greater than 90° and less than 180°. For example; a slice of watermelon is an obtuse angle triangle.
Triangles and special relations in math
In the dense world of mathematics, triangles classification is beyond the basics now. This reading covers every aspect of the thrilling world of triangles in geometry. Let’s find out the special relations of triangles with me.
- Pythagorean Theorem – Who doesn’t know about this famous theorem? I think we all are familiar with this. This theorem is all about the sides of a right angle triangle. In an isosceles right triangle, the square of hypotenuse is equivalent to the sum of perpendicular and base. (a^2 + b^2 = c^2)
- 30°-60°-90° Triangle – Triangle has these special angles. 30, 60 and 90. The ratio is fixed and specific between the sides of the triangle. The shorter leg is opposite the 30 degrees, the longer leg is opposite the 60 degrees and the hypotenuse is totally opposite the 90 degree angle.
- Similar Triangles – Every triangle is the same if their corresponding triangles are equal. Even if the sides are of different length. For example; imagine a balloon. The blown up balloon is exactly the same as the original one. It goes similarly for triangles.
Formulation Of A Triangle
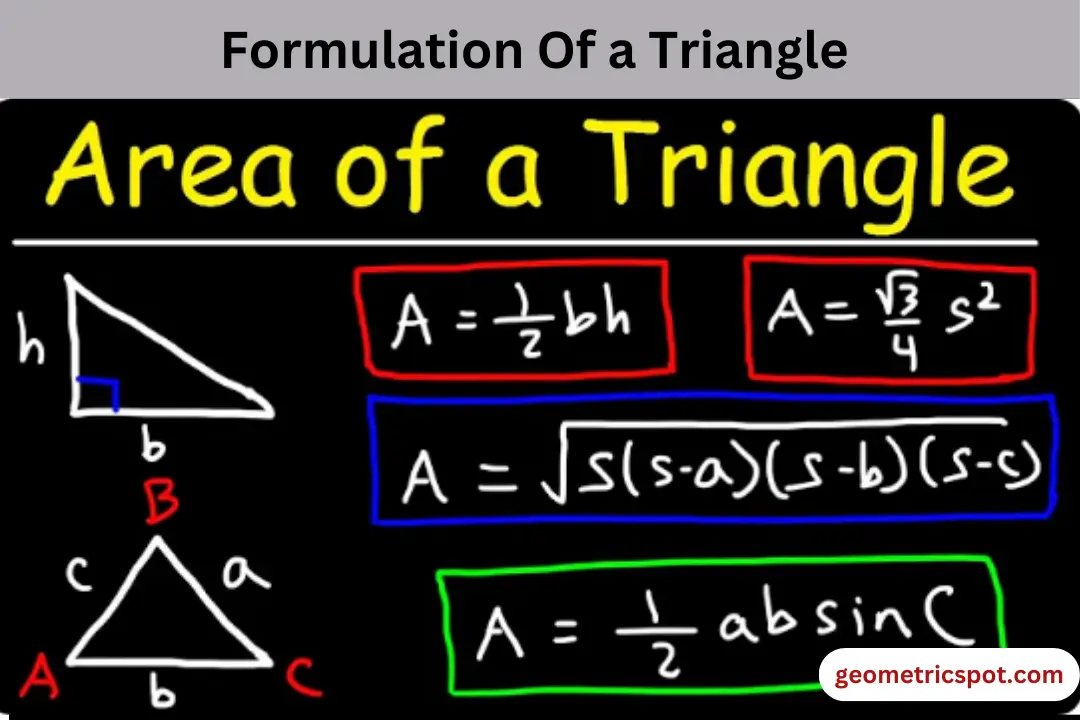
Suppose h is the hypotenuse, p is the perpendicular and b is the base. Formula to find the area of a triangle should be:
Area of a triangle = ½ square units
If h, p and b are the sides of a triangle, then the formula to find the perimeter of a triangle should be:
Perimeter of a triangle = p + b + h units
Qualities and properties of a triangle
- How a bridge can be stable or a roof rely on the material all depends upon triangles. Triangles play a vital role in the field of architecture.
- Artists and painters use triangles to create balance, dynamic compositions and implement different ideas in their art.
- From simple tools like scissors to heavy machinery like airplanes uses the properties of triangles to be functional.
- Whenever you add any two sides of a triangle, it’s greater than the third side.
- We can say that two triangles are the same if the corresponding angles are congruent and the corresponding length of the sides are proportional.
Conclusion
When you will dive into the thrilling world of triangles. Remember one thing that these wonders are just beyond the shapes. These are the basic building blocks and foundations of mathematics. From navigating the trigonometric laws to exploring the symmetry of nature, triangles are everywhere to help you. These wonders are not limited to theories, it’s about balance, construction, architecture, art and strength.
The thrilling world of triangles in geometry is something everyone must be curious about to learn. Start your exploration, learn throughout the journey with this article and admire the simplicity and beauty of triangles.
Frequently asked questions
How can triangles be implied in our daily lives?
Have you ever seen traffic lights? The most common implementation of a triangle. Bed, glass, mirror, laptop and many more things originated from angles and triangles. Read this guide about the thrilling world of triangles to understand the concept and implementation. Pyramids, sailing boats, truss bridges, and rooftops are basic usage of triangles.
What is the basic concept of a triangle?
Every triangle has three sides and three angles. The sum of all three sides is equivalent to 180 degrees. The exterior angles always give a sum of 360°. And whenever we will add interior and exterior angles, we will get a supplementary angle.
What is the vertex in a triangle?
Vertex is a point of intersection where two lines or sides cut each other or meet each other. Every triangle has 3 vertices called ABC.
