Circle Geometry for Beginners | Formulas, Properties & Parts Of Circle

Circles! The round appearance we saw everywhere. From the planet we are living to the tortilla we are eating, circles are everywhere. But what exactly is a circle? How can we measure the size of a circle? How to understand the basics of a circle?

Let’s explore the definitions, types, properties, and formulas of a circle with examples. Tighten your seat belts because we are going to embark on a journey of circle geometry for beginners with Formulas, Properties & Parts Of Circle .

The Circles

https://geometricspot.com/what-are-the-types-of-angles-in-geometry Circles belong to the family of two dimensional geometry. 2D means that you can draw them on a plain piece of paper. This two-dimensional diagram has area and perimeter. It is defined as the collection of multiple points that are placed at the same distance away from a fixed point called center.

In other words, we can say that a circle is a continuous or unbroken line that curves back to itself. It means circles are a closed loop. Moreover, circles don’t have any corners or edges like squares and triangles.

What makes them apart? Their smooth nature makes them unique and different. Every dot or line that passes through every point of circle forms a line of reflection symmetry. Circles have rotational symmetry around every angle.

Round or circular objects

There are unlimited things in our surroundings which are based on a circle or a circle. Some common examples are:

• Wedding rings
• Pizza
• Coins
• Wheels or tyres
• Buttons
• Lolly pop
• CD or DVD
• Balls
• Tables

How to draw a circle as a beginner?

Mastering the art of drawing a circle is as easy as eating pizza. These trips and tricks about circle geometry as a beginner will definitely help you to draw a circle. Here are a few tips and methods to draw a circle as a beginner.

• The compass method – Take a paper and mark a dot somewhere on the paper. Give it a name of your choice. Open the compass according to the size of the circle. In this case, I am opening 4cm. Place the tip of the compass at the marked dot and draw a circle.
• Round cap or coin – Use any round object from your surroundings. Place on a plane paper and draw a circle.

Parts Of Circle

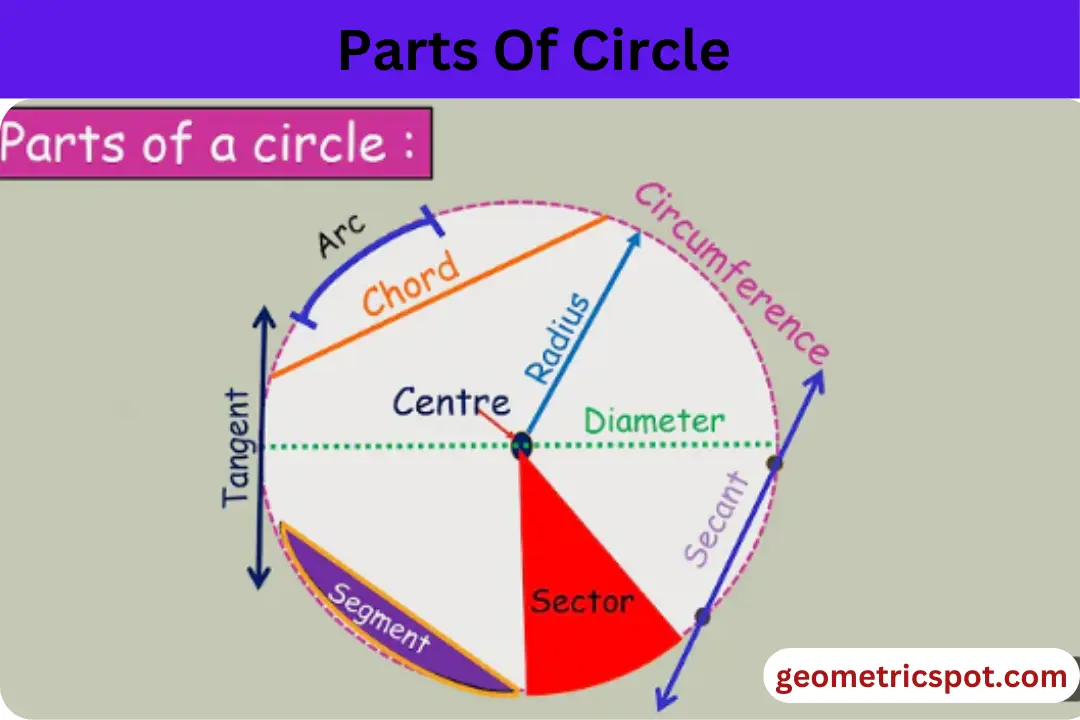
These are the basic parts of circle beginners must know about:

• Centre (O) – The midpoint of a circle or a fixed point from which all other points locate at the same distance away. Imagine the bullseye of a target. It’s the center.

• Radius (r ) – The half of a circle or diameter is called a radius. Or a distance from the center (O) to any point located anywhere of the circle’s outline ( circumference). For example; a bike wheel – the distance from the hub to the rim.

• Diameter (d) – A straight line that starts from any point of the circle’s edge and ends at the opposite side of the circle’s outline. In other words, a line passes or connects both  ends of the circle. It is also the largest chord of the circle.

• Circumference (c ) – The total length of the circle’s outline or edge is called circumference. Or it is defined as the distance around the circle. It represents the entire length of the circle. Perimeter also refers to circumference.

• Tangent –  A straight line that touches the circle or outline of a circle at any point is called tangent.

• Secant – A straight line passing through two points of circle or cutting two points of a circle is called secant.

• Chord – A line that joins any two points located anywhere at the circle’s edge is called chord.

• Annulus – The common area between two concentric circles is called annulus.

• Arc – A part of circumference or a smooth curve line that joins two endpoints.

• Sector – Sector refers to the area or part of a circle that is made with arc and two radii.

• Segment – A separate region between a circle that can be bounded by a chord and an arc is called segment.

Formulas of circle

The formula of circle in the plane is:

(x-h)^2 + (y-k)^2 = r^2 

x and y are the points of coordinates on the plane whereas h and k refer to the coordinate center of the circle. Radius is described as r in this formula.

The formula for finding a diameter of circle is :

d = 2r

The formula for finding radius of a circle is:

r = d/2

The formula for finding circumference of a circle is:

c = πd = 2πr

Or

c = 2πr

Value of π = 3.14159 ( roughly equivalent)

The formula for finding area of a circle is:

a = πr^2

Different Properties Of Circle

Circle holds many fascinating and attractive properties such as:

• Circles are called the perfect symmetric shapes. Draw a diameter into any direction or from any point, it will give the same answer. It will divide the circle into two equal halves. For example; Cutting a fully round pizza into half.

• Diameter of a circle is the largest chord.

• Circles with equal radii are congruent to each other or different sizes of circles having different radii are similar in nature.

• A straight line that touches the circle at any point is called tangent. Just imagine a line that touches a ball. This line is always perpendicular at 90° angle.

• All time constant circumference to diameter ratio. Beyond the size of a circle, π (c/d = π). In simple words, the ratio of circumference to its diameter is always constant.

Final Words

Circles just don’t belong to math. They are everywhere. From gears and wheels to clocks and watches. Mathematicians and artists are using these shapes to build, construct and draw endless things. Learn the formulas in this article and practice to make your concepts clearer.

This guide about circles geometry for beginners with Formulas, Properties & Parts Of Circle will help you to clear your concepts. Learn, learn and learn is the only formula which helps you to gain knowledge.