All About Lines and Angles In Geometry | Types, Properties & Practice Questions & Answers
Lines and angles are considered the fundamental shapes in geometry. Geometry is the study of how forms, sizes, spaces, and positions of things relate to each other. All of them are made up of lines, angles, and points, which makes it easy to describe their shapes and sizes.
A point is something that doesn’t have any parts in mathematics. This is shown by a dot. When you connect two separate points, you get a line. A line can be stretched forever because it doesn’t have any ends.
A line segment is the part of a line that has two ends. Ray is also a part of the line that doesn’t have any other ends. An angle is a shape where two rays come out of the same point. In this article we will discuss the All About Lines and Angles In Geometry | Types, Properties & Practice Questions & Answers in geometry.
What are Lines?

Lines are defined as a series of small, almost imperceptual points. One can extend a line including two arrowheads in either direction. Conversely, a segment is a defined finite space formed between two locations.
One cannot extend it in either direction. Its length is computed on a subset of the line. Students have been seen to regularly confuse lines and segments. Lines and segments differ mostly from one another in that the former can be stretched while the latter has a set length. The chapter on class 3 lines and point angles illustrates this difference. Also 7REELZ APP.
Types of Lines
Vertical line:
That line occurs on the vertical plane. Regarding orientation, it runs north to south. Said another way, it’s a line that spans the top to the bottom of the page.
Horizontal line:
It is a line that exists on the horizontal plane. Regarding direction, it goes East to West. All responded, it is a line spanning the left to the right side of the page.
Parallel Line:
A parallel line is formed when two lines run in the same direction without crossing or meeting. Though they will never cross, these lines can be stretched indefinitely.
Perpendicular Line:
When two straight lines intersect at a 90-degree angle, they are said to be parallel to each other. Their angle is also sometimes known as a right angle. Their point of intersection is that which they cross. Four right angles create themselves at the junction of two perpendicular lines.
What are Rays?
Though it has a fixed starting point and can only be stretched endlessly in one direction, a ray is like a line. In the introduction to angles, rays are essential.
What are Angles?
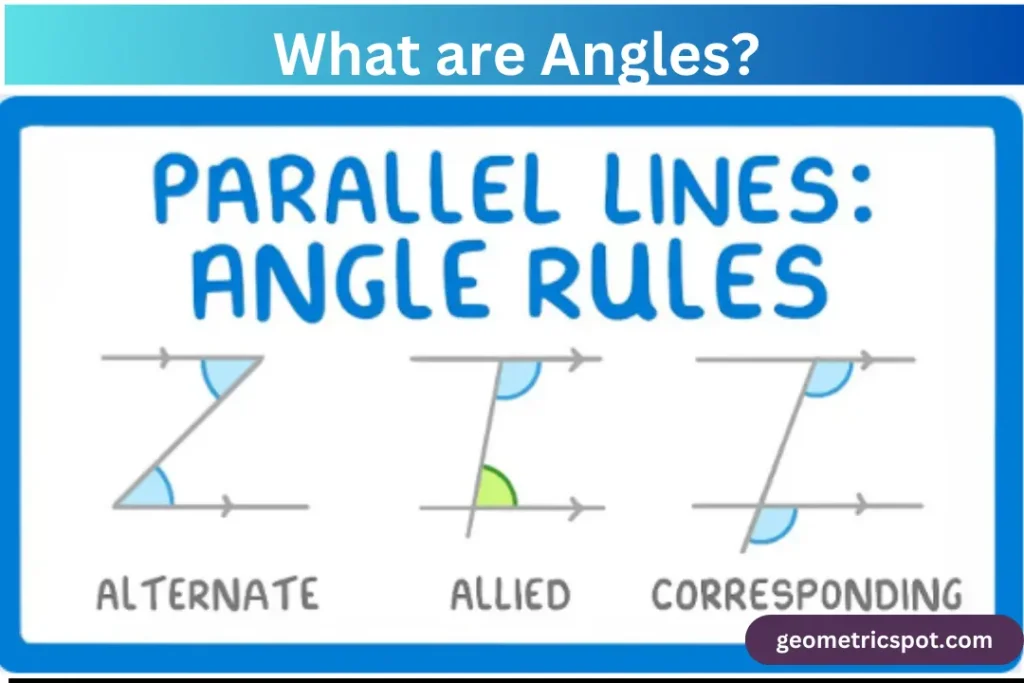
An angle is an area created by two rays sharing the same vertex. From their ends, the two rays can be stretched in the pointed arrow’s stated direction.
Types of Angles
Geometry uses several kinds of lines and angles depending on the measurements and other situations.
Let us learn here all those lines and angles together with their definitions.
- Acute Angle
- Obtuse Angle
- Right angle
- Straight Angle
- reflex angle
- Complete Angle
Acute Angle:
An acute angle is that which is smaller than a right angle. It gauges from 0 degrees to 90 degrees. The acute angle graphic below illustrates:
Obtuse Angle:
An angle is said to be obtuse when its measure exceeds a right angle. It’s more than ninety degrees. The picture below features an obtuse angle:
Right angle:
An angle is said to be a right angle when its measure exactly 90 degrees.
Straight Angle :
The straight angle is the angle so produced if an angle’s measurement is 180 degrees. The straight angle picture that is put below
Reflex Angle:
Reflex Angle is the measurement of the angle when it is less than 360° and more than 180°. The Reflex Angle picture that is below
Complete Angle:
The angle is said to be Complete Angle when its measurement is 360°. The Complete Angle picture that is uploaded below
Properties of Lines and Angles

Lines and angles have inherent qualities, much as other forms and sizes in geometry. Let’s see what they are.
Properties of Lines
- Collinear points are three or more points arranged on the same line.
- Non-collinear points are those which do not lie on the same line.
Properties of Angles
- An angle is a figure wherein two rays arise from a same point. The vertex of the angle is this point; the two rays making the angle are its sides or arms.
- Reflex angles are those which lie between 180 degrees and less than 360 degrees.
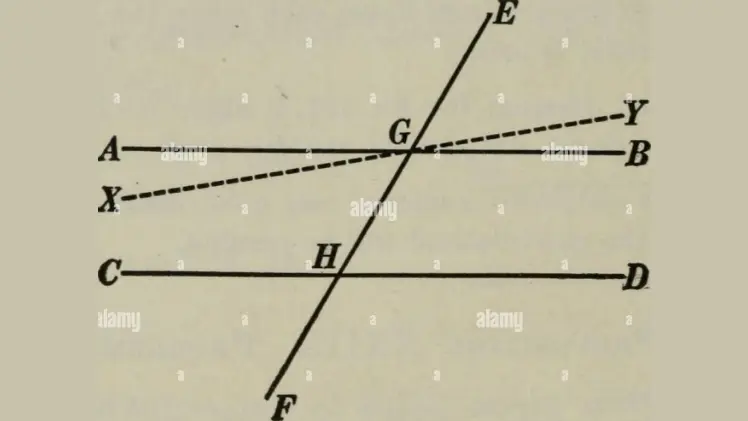
- Two adjacent angles are a linear pair of angles if their sum equals 180 degrees. A and b create a linear pair in the figure that follows.
- Vertically opposing angles are the two opposite sets of angles produced when two lines cross each other. ∠A and ∠B in the next illustration are vertically opposing angles. Still another pair are ∠C and ∠D.
Lines and Angles Practice Questions with Answers
Question 1
What is the measure of each angle in a pair of complementary angles if one angle is twice the other?
Answer:
Let the measure of the smaller angle be xxx.
Then the measure of the larger angle is 2x2x2x.
Since they are complementary angles, their sum is 90∘90^\circ90∘:
x+2x=90∘x + 2x = 90^\circx+2x=90∘ 3x=90∘3x = 90^\circ3x=90∘ x=30∘x = 30^\circx=30∘
So, the smaller angle is 30∘30^\circ30∘ and the larger angle is 60∘60^\circ60∘.
Question 2
If two parallel lines are cut by a transversal, and one of the alternate interior angles is 70∘70^\circ70∘, what is the measure of the other alternate interior angle?
Answer:
If two parallel lines are cut by a transversal, alternate interior angles are equal.
Thus, the measure of the other alternate interior angle is 70∘70^\circ70∘.
Question 3
Find the measure of an angle which is 20∘20^\circ20∘ less than its supplement.
Answer:
Let the measure of the angle be xxx.
Then its supplement is 180∘−x180^\circ – x180∘−x.
According to the problem,
x=(180∘−x)−20∘x = (180^\circ – x) – 20^\circx=(180∘−x)−20∘ x=160∘−xx = 160^\circ – xx=160∘−x 2x=160∘2x = 160^\circ2x=160∘ x=80∘x = 80^\circx=80∘
So, the measure of the angle is 80∘80^\circ80∘.
Question 4
In a triangle, one angle is 90∘90^\circ90∘ and another angle is 45∘45^\circ45∘. What is the measure of the third angle?
Answer:
The sum of the angles in a triangle is 180∘180^\circ180∘.
Let the measure of the third angle be xxx.
90∘+45∘+x=180∘90^\circ + 45^\circ + x = 180^\circ90∘+45∘+x=180∘ 135∘+x=180∘135^\circ + x = 180^\circ135∘+x=180∘ x=45∘x = 45^\circx=45∘
So, the measure of the third angle is 45∘45^\circ45∘.
Question 5
Two angles are supplementary. One angle is 5∘5^\circ5∘ more than three times the other. Find the measures of the angles.
Answer:
Let the measure of the smaller angle be xxx.
Then the measure of the larger angle is 3x+5∘3x + 5^\circ3x+5∘.
Since the angles are supplementary, their sum is 180∘180^\circ180∘:
x+(3x+5∘)=180∘x + (3x + 5^\circ) = 180^\circx+(3x+5∘)=180∘ 4x+5∘=180∘4x + 5^\circ = 180^\circ4x+5∘=180∘ 4x=175∘4x = 175^\circ4x=175∘ x=43.75∘x = 43.75^\circx=43.75∘
So, the smaller angle is 43.75∘43.75^\circ43.75∘ and the larger angle is:
3x+5∘=3(43.75∘)+5∘=131.25∘3x + 5^\circ = 3(43.75^\circ) + 5^\circ = 131.25^\circ3x+5∘=3(43.75∘)+5∘=131.25∘
So, the measures of the angles are 43.75∘43.75^\circ43.75∘ and 131.25∘131.25^\circ131.25∘.
Question 6
In a quadrilateral, two angles are 90∘90^\circ90∘ each, and the third angle is 110∘110^\circ110∘. Find the measure of the fourth angle.
Answer:
The sum of the angles in a quadrilateral is 360∘360^\circ360∘.
Let the measure of the fourth angle be xxx.
90∘+90∘+110∘+x=360∘90^\circ + 90^\circ + 110^\circ + x = 360^\circ90∘+90∘+110∘+x=360∘ 290∘+x=360∘290^\circ + x = 360^\circ290∘+x=360∘ x=70∘x = 70^\circx=70∘
So, the measure of the fourth angle is 70∘70^\circ70∘.
Question 7
Two angles are complementary. One angle is 10∘10^\circ10∘ more than the other. Find the measures of the angles.
Answer:
Let the measure of the smaller angle be xxx.
Then the measure of the larger angle is x+10∘x + 10^\circx+10∘.
Since the angles are complementary, their sum is 90∘90^\circ90∘:
x+(x+10∘)=90∘x + (x + 10^\circ) = 90^\circx+(x+10∘)=90∘ 2x+10∘=90∘2x + 10^\circ = 90^\circ2x+10∘=90∘ 2x=80∘2x = 80^\circ2x=80∘ x=40∘x = 40^\circx=40∘
So, the smaller angle is 40∘40^\circ40∘ and the larger angle is 50∘50^\circ50∘.
Question 8
Find the measure of an angle that is three times its complement.
Answer:
Let the measure of the angle be xxx.
Then its complement is 90∘−x90^\circ – x90∘−x.
According to the problem,
x=3(90∘−x)x = 3(90^\circ – x)x=3(90∘−x) x=270∘−3xx = 270^\circ – 3xx=270∘−3x 4x=270∘4x = 270^\circ4x=270∘ x=67.5∘x = 67.5^\circx=67.5∘
So, the measure of the angle is 67.5∘67.5^\circ67.5∘.
Question 9
The ratio of two complementary angles is 2:3. Find the measures of the angles.
Answer:
Let the measures of the angles be 2x2x2x and 3x3x3x.
Since the angles are complementary, their sum is 90∘90^\circ90∘:
2x+3x=90∘2x + 3x = 90^\circ2x+3x=90∘ 5x=90∘5x = 90^\circ5x=90∘ x=18∘x = 18^\circx=18∘
So, the measures of the angles are:
2x=2(18∘)=36∘2x = 2(18^\circ) = 36^\circ2x=2(18∘)=36∘ 3x=3(18∘)=54∘3x = 3(18^\circ) = 54^\circ3x=3(18∘)=54∘
So, the measures of the angles are 36∘36^\circ36∘ and 54∘54^\circ54∘.
Question 10
In a linear pair, if one angle is 70∘70^\circ70∘, find the measure of the other angle.
Answer:
In a linear pair, the angles are supplementary, so their sum is 180∘180^\circ180∘.
Let the measure of the other angle be xxx.
70∘+x=180∘70^\circ + x = 180^\circ70∘+x=180∘ x=110∘x = 110^\circx=110∘
So, the measure of the other angle is 110∘110^\circ110∘.
FAQ’s
What are the lines about angles?
A geometric figure known as an angle is created when two lines cross in the same plane. An angle’s point of intersection is known as its vertex, and the lines that line up the angle are known as its arms, or sides.
What are the line and angle facts?
Angles add up to 360° when they fill the area surrounding a point and share a vertex. It is equal to the against angle when two lines cross. Alternate angles are equivalent when a line crosses parallel lines. The corresponding angles of two lines that cross one other are equal.
What does the term “lines” mean?
One-dimensional figures with length but no width are called lines. A collection of points that are endlessly stretched in opposing directions make up a line. Two points in a two-dimensional plane determine it. Collinear points are those that are located on the same line.