A Simple Introduction to Polar Coordinates | Formulas, Examples & Practice Tasks
Polar coordinates! A word that sounds tricky and difficult but believe me, it’s easy peasy lemon squeezy. Generally, polar coordinates is a system of locating points in a plane with a reference point O.
In this article, we will give you the basic understanding of a Simple Introduction to Polar Coordinates | Formulas, Examples & Practice Tasks. Moreover, you will see the practical implementations of polar coordinates.
What is a Polar Coordinate?

Pole – the reference point
Polar coordinate is a method to explain the location of a point in a plane. It’s different from the Cartesian plane coordinates which use the x and y axis. Polar coordinates use a distance from a fixed point and an angle from a fixed direction. The coordinates are written in r and (θ).
- Radius (r) – A distance from a fixed point to the origin.
- Angle (θ) – It’s the angle made between a positive x-axis and the line connecting the origin to the point.
In simple words, each and every point on a plane of a two-dimensional coordinate system is evaluated by a distance from a reference point and an angle taken from a reference direction is called polar coordinate system.
Polar Coordinate Formula
We can write and find infinite numbers of polar coordinates for a single coordinate point. By using this formula:
(r, ô + 2πn) or (-r, o + (2n + 1) π)
- n is representing the integer.
- Thetha’s value will be positive if it is measured counterclockwise
- Thetha’s value will be negative if it is measured clockwise.
- The value of r will be positive if taken from the terminal side of (θ).
- The value of r will be negative if taken from the origin side of theta.
Important Note
The side of the plane where the angle contempt is called the initial side.
Why use polar coordinates?
Normally, we use polar coordinates specifically in the scenarios where the relationship between points is more naturally expressed in terms of angles and distances.
For instance;
They are frequently used in physics, engineering and navigation.
For more information and knowledge read my recent article Reflexive Property in Geometry | Congruence, Proof & Examples
How to plot points in polar coordinates?
To plot a point in polar coordinates, you need to understand radius and angle.
For instance;
The point (5,45°) is 5 units away from the origin. It forms an angle 45° with the positive x-axis.
How to convert between polar and Cartesian coordinates?

It’s a basic understanding. You must know about the conversion between Cartesian and polar coordinates. It’s a step-by-step guide to convert between polar and Cartesian coordinates.
From polar to Cartesian
To convert polar coordinates (r,θ) to Cartesian coordinates (x,y):
x = r cos (θ)
y = r sin (θ)
From Cartesian to polar
To convert Cartesian coordinates (x,y) to polar coordinates (r, θ):
r = √x^2 + y^2
θ = tan^-1 (x/y)
Real-World Examples of Polar Coordinates
- Navigation
Imagine I am a sailor and trying to navigate in the ocean. Instead of saying “go 5 miles east and 6 miles north” (Cartesian), you can say “sail 5 miles at an angle of 53 degrees” (polar).
- Spiral Pattern
Polar coordinates are perfect for explaining spirals. For example, the equation r=θr = \theta=θ explains a spiral where the radius increases as the angle increases.
For more information and knowledge read my recent article Exploring the Geometry Of Circles: Tangents, Secants & Chords With Examples
Fun Facts about Polar Coordinates
- Like polar bears live near the poles. Polar coordinates revolve around the pole or origin point.
- We use polar coordinates to express art and craft such as: they are used in computer graphics to create patterns.
- Stars and planets are plotted through polar coordinates. People who believe in astronomy used polar coordinates to express stars in the sky.
Practice tasks of polar coordinates
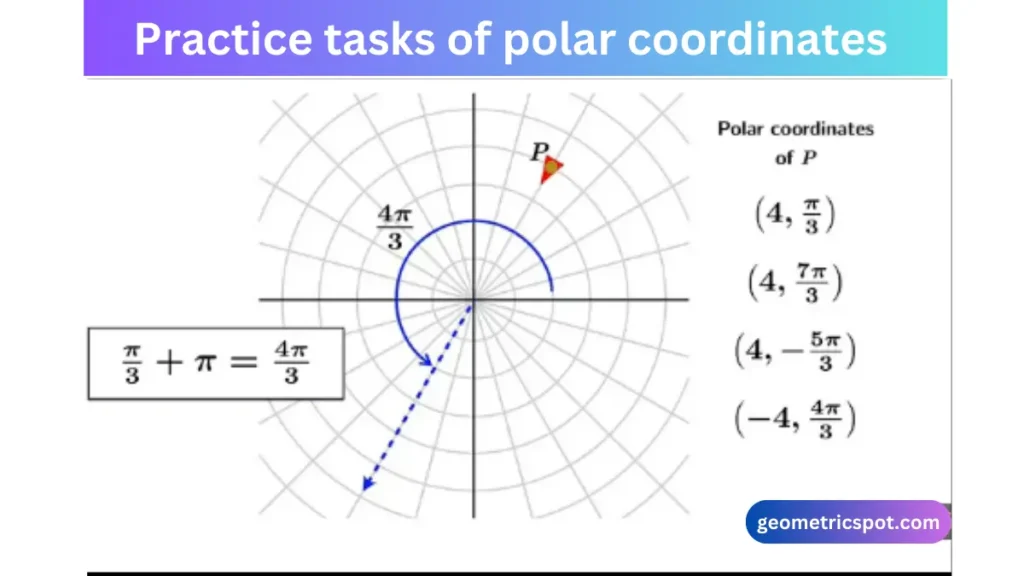
To practice problems of polar coordinates, you must try solving these.
Problem : 1
Convert the Cartesian coordinates (3,4)(3, 4) to polar coordinates.
r = √3^2 + 4^2
r = √9 + 16
r = √25
r = 5
θ = tan^-1 (4/3)
θ = 53.13°
So, the polar coordinates are 5, 53.13°.
Problem : 2
Convert the polar coordinates (7,60°) to Cartesian coordinates.
x = 7 cos (60°)
7*0.5 = 3.5
y = 7 sin (60°)
7*√3/2 = 6.06
So, the Cartesian coordinates are 3.5, 6.06.
Tips to learn about polar coordinates
- Practice, Practice, and Practice: The more you work with polar coordinates, the more comfortable you’ll become. Practice the above -mentioned problems and change the values.
- Use Visual Aids: Graphing polar coordinates can help you understand the relationships between radius, angle, and position. Radius, angle and origin are the 3 basic understandings one must have.
- Remember the Quadrants: Keep in mind which quadrant you are in to ensure the angle θ is correct.
Final Words
It’s a powerful way to express the position of points in a plane. From describing navigation to designing digital prints or exploring the knowledge about stars and planets, it will help you throughout mathematics. Understanding polar coordinates can open up a world of possibilities. Practice is a key to success. Stay curious and learn new inventions about polar coordinates.
Frequently asked questions
What is the effect of polar coordinates?
It’s a useful tool to create a distorted effect of an image or a video. It can switch the position of the characters along the x-axis and y-axis.
Can a polar coordinate be a negative?
Yes, if the measurements of an angle is taken in a clockwise direction, the angle will be negative.
Is there any benefit of polar coordinates?
Yes, there are many benefits of polar coordinates in mathematics and the real-world. You can use the polar coordinates formula to solve equations and problems. You can use polar coordinates to describe the navigation and draw the digital image of structures.