Reflexive Property in Geometry | Congruence, Proof & Examples
Geometry is a field of mathematics that deals with shapes, sizes, and the properties of space. One of the fundamental concepts in geometry is the idea of congruence, which essentially means that two shapes are identical in form and size.
Within the realm of congruence, the reflexive property plays a crucial role. This article will deliver into what the reflexive property is, Reflexive Property in Geometry | Congruence, Proof & Examples , explain how to prove it, and offer some examples to illustrate its application.
What Is Reflexive Property?
The reflexive property is a principle stating that any geometric figure is congruent to itself. In simpler terms, it means that any shape or object is always equal to itself. This might seem obvious, but it’s an essential building block in the study of geometry and proofs.
Mathematically, the reflexive property can be written as: a=aa = aa=a where aaa is any geometric figure. This property is one of the fundamental properties of equality and is used extensively in geometric proofs.
Reflexive Property of Congruence

In the context of congruence, the reflexive property states that any geometric figure is congruent to itself. This is particularly important when working with triangles, angles, line segments, and other geometric shapes.
For example:
consider a triangle △ABC\triangle ABC△ABC.
According to the reflexive property of congruence, we can say: △ABC≅△ABC\triangle ABC \cong \triangle ABC△ABC≅△ABC This means that triangle △ABC\triangle ABC△ABC is congruent to itself, highlighting the inherent equality of the shape with itself.
Proof of the Reflexive Property with Examples
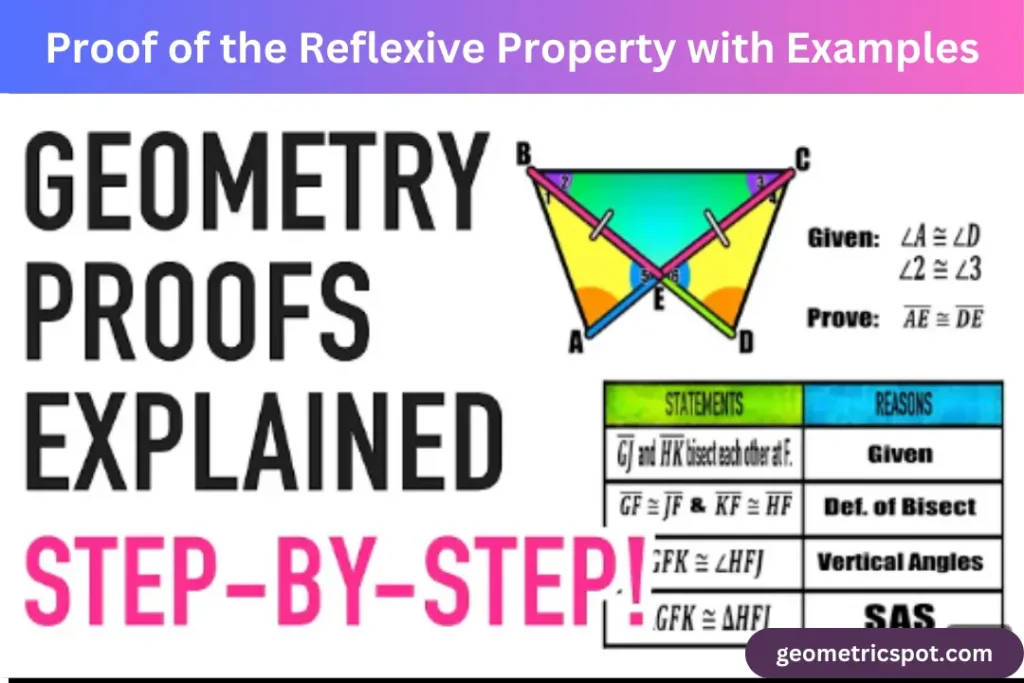
Proving the reflexive property is straightforward due to its self-evident nature. In geometry, a proof often involves showing that a statement is universally true based on previously established axioms and theorems.
To prove the reflexive property of congruence for a geometric figure, you can follow these steps:
- Identify the Geometric Figure: Start by selecting any geometric figure, such as a triangle, angle, or line segment.
- Apply the Reflexive Property: State that the figure is congruent to itself. For example, if you have a line segment ABABAB, you would write: AB‾≅AB‾\overline{AB} \cong \overline{AB}AB≅AB
- Justify the Statement: Explain that by the definition of the reflexive property, any figure is congruent to itself. This step often involves citing the property itself as the reason.
Because the reflexive property is a fundamental axiom, its proof is inherently simple and universally accepted without further justification.
Examples of the Reflexive Property
Example 1: Line Segments
Consider the line segment XY‾\overline{XY}XY. According to the reflexive property of congruence, we can state that: XY‾≅XY‾\overline{XY} \cong \overline{XY}XY≅XY This example shows that the line segment is congruent to itself, which is a straightforward application of the reflexive property.
Example 2: Angles
Now, consider an angle ∠PQR\angle PQR∠PQR. By the reflexive property, we know that: ∠PQR≅∠PQR\angle PQR \cong \angle PQR∠PQR≅∠PQR This indicates that the angle is congruent to itself, reinforcing the idea that any geometric figure is equal to itself.
Example 3: Triangles
Finally, consider a triangle △DEF\triangle DEF△DEF. Using the reflexive property of congruence, we can assert that: △DEF≅△DEF\triangle DEF \cong \triangle DEF△DEF≅△DEF This demonstrates that the triangle is congruent to itself, highlighting the reflexive property in the context of a more complex geometric shape.
Importance of the Reflexive Property in Geometry
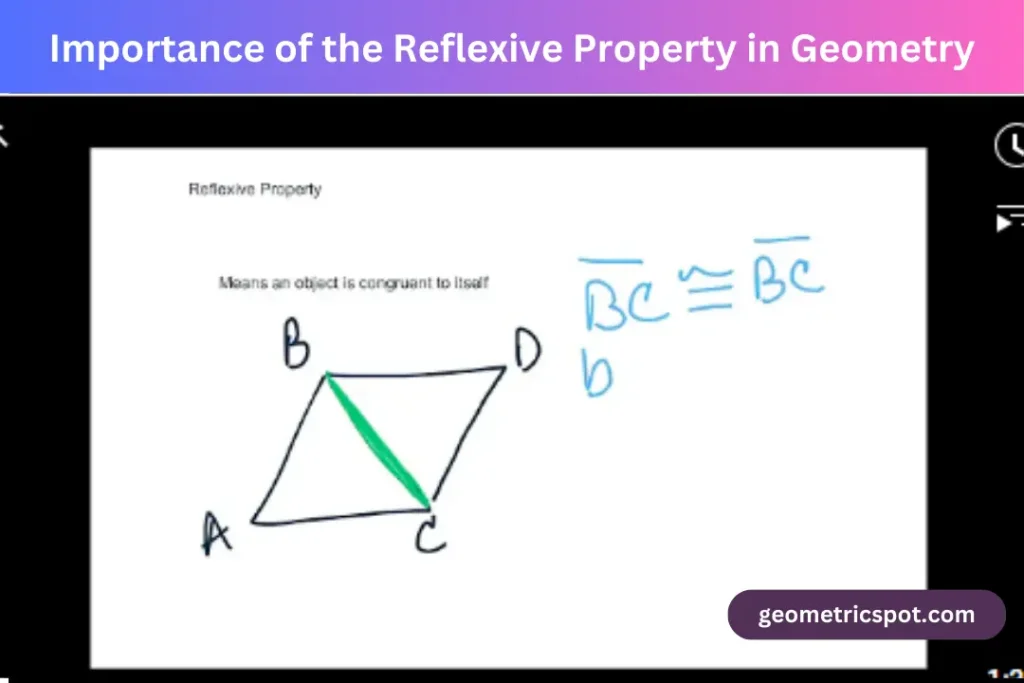
The reflexive property is foundational in geometry because it establishes the basic notion of equality and congruence within geometric figures. It serves as a building block for more complex proofs and theorems, enabling mathematicians to demonstrate relationships and properties of geometric shapes systematically.
In geometric proofs, the reflexive property is often used as a stepping stone to prove other properties and relationships.
For instance, when proving that two triangles are congruent using the Side-Angle-Side (SAS) Postulate, the reflexive property might be used to show that a shared side is equal to itself, thereby satisfying one of the conditions of the postulate.
Conclusion
The reflexive property is a simple yet powerful concept in geometry. It asserts that any geometric figure is congruent to itself, providing a foundational principle for proving more complex geometric relationships. By understanding and applying the reflexive property, students and mathematicians can build a solid framework for exploring the intricate world of geometric shapes and their properties.
Whether dealing with line segments, angles, or triangles, the reflexive property is a key tool in the geometric toolkit, underscoring Reflexive Property in Geometry | Congruence, Proof & Examples inherent equality of shapes and aiding in the construction of logical and rigorous proofs.